Majorana equation

The Majorana equation is a relativistic wave equation similar to the Dirac equation but includes the charge conjugate ψ_c of a spinor ψ. It is named after the Italian physicist Ettore Majorana, and it is

$-i {\partial\!\!\!\big /} \psi %2B m \psi_c = 0 \qquad \qquad (1)$

written in Feynman notation. Here ψ_c is the `charge conjugate' of ψ, which can be defined in the Majorana basis as

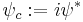$\psi_c�:= i \psi^*\$ .

Equation (1) can alternatively be expressed as

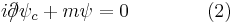$i {\partial\!\!\!\big /} \psi_c %2B m \psi = 0 \qquad \qquad (2)$ .

In either case, the quantity m in the equation is called the Majorana mass.

The appearance of both ψ and ψ_c in the Majorana equation means that the field ψ cannot be coupled to an electromagnetic field without violating charge conservation, so ψ is taken to be neutrally charged. Nonetheless, the quanta of the Majorana equation given here are two particle species, a neutral particle and its neutral antiparticle. The Majorana equation is frequently supplemented by the condition that ψ = ψ_c (in which case one says that ψ is a Majorana spinor); this results in a single neutral particle. For a Majorana spinor, the Majorana equation is equivalent to the Dirac equation.

Particles corresponding to Majorana spinors are aptly called Majorana particles. Such a particle is its own antiparticle. Thus far, of all the fermions included in the Standard Model, none is described as a Majorana fermion. However, there is the possibility that the neutrino is of a Majorana nature. If so, neutrinoless double-beta decay is possible. A number of experiments probing if the neutrino is a Majorana particle are currently underway.^[1]

References

^ Franklin, A: Are there really neutrinos?: an evidential history, page 186. Westview Press, 2004.

Majorana equation

See also

References

External links